Handle decompositions of 3-manifolds
In mathematics, a handle decomposition of a 3-manifold allows simplification of the original 3-manifold into pieces which are easier to study. An important method used to decompose into handlebodies is the Heegaard splitting, which give us a decomposition in two handlebodies of equal genus.[1]
As an example: lens spaces are orientable 3-spaces, and allow decomposition into two solid-tori which are genus-one-handlebodies. The genus one non-orientable space is a space which is the union of two solid Klein bottles and corresponds to the twisted product of the 2-sphere and the 1-sphere: 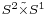 .
.
Each orientable 3-manifold is the union of exactly two orientable handlebodies; meanwhile, each non-orientable one needs three orientable handlebodies.
The minimal genus of the glueing boundary determines what is known as the Heegaard genus. For non-orientable spaces an interesting invariant is the tri-genus.
References
- ^ Turaev, Vladimir G. (1994). Quantum Invariants of Knots and 3-manifolds. Walter de Gruyter. ISBN 3110137046.
- J.C. Gómez Larrañaga, W. Heil, V.M. Núñez. Stiefel-Whitney surfaces and decompositions of 3-manifolds into handlebodies, Topology Appl. 60 (1994), 267-280.
- J.C. Gómez Larrañaga, W. Heil, V.M. Núñez. Stiefel-Whitney surfaces and the trigenus of non-orientable 3-manifolds, Manuscripta Math. 100 (1999), 405-422.